A Bayesian analysis of polls in the Catalan elections
(Invited post by Virgilio Gómez-Rubio, UCLM, Albacete, Spain. Thanks Gianluca for the invitation!!)
I have been involved in the planning and analysis or survey polls almost since I came back to Albacete 9 years ago. Last months in Spanish politics have been dominated by the ‘Catalan referendum’ and the call for new elections from the national government via article 155 in the Spanish Constitution (which had never been enforced before). This elections have been different for many reasons, so I decided to do a (last minute) analysis of the available polls to try to predict the allocation of seats in the elections.
The Catalan parliament has 135 seats, split in four electoral districts which correspond to the four provinces in the region, with different number of seats depending on their population: Barcelona (85 seats), Gerona (17 seats), Lérida (15 seats) and Tarragona (18 seats). Seats are allocated according to the D’Hondt method.
Several polls have been published in the mass media, and the proportions of votes to parties (as well as sample size, etc.) are either reported at the regional level (which is useless to allocate seats per provinces) and province level. Given that most polls are aggregated at the regional level it makes sense to combine both types of polls into a single model to provide some insight on the voters’ preferences at the province level to allocate the number of seats.
Bayesian hierarchical models are great at combining information from different sources. The model that I have considered now is very simple. The number of votes (reported in the poll) to each party at the regional level are assumed to follow a multinomial distribution with probabilities \(P_i, i=1,\ldots, p\), where \(p\) is the number of political parties. In this case, we have 7 main parties plus another group for ‘other parties’. Probabilities \(P_i\) are assigned a vague Dirichlet prior. The number of votes at the province level are assumed to follow a multinomial distribution as well, with probabilities \(p_{i,j},\ i=1,\ldots,p, j=1,\ldots,4.\). Both probabilities are linked by assuming that \(\log(p_{i,j})\) is proportional to \(\log(P_i)\) plus a province-party specific random effect \(u_{i,j}\). I have used this model before with good results.
As simple as it is, this model allows the combination of polls at different aggregation levels. I have used JAGS to fit the model and to allocate the number of seats by exploiting the probabilities from the MCMC output to obtain 10000 draws of the allocation of seats by applying D’Hont rule to the proportion of votes to each party at the proven level.
Next plot shows the distribution of seats against the actual distribution of seats:
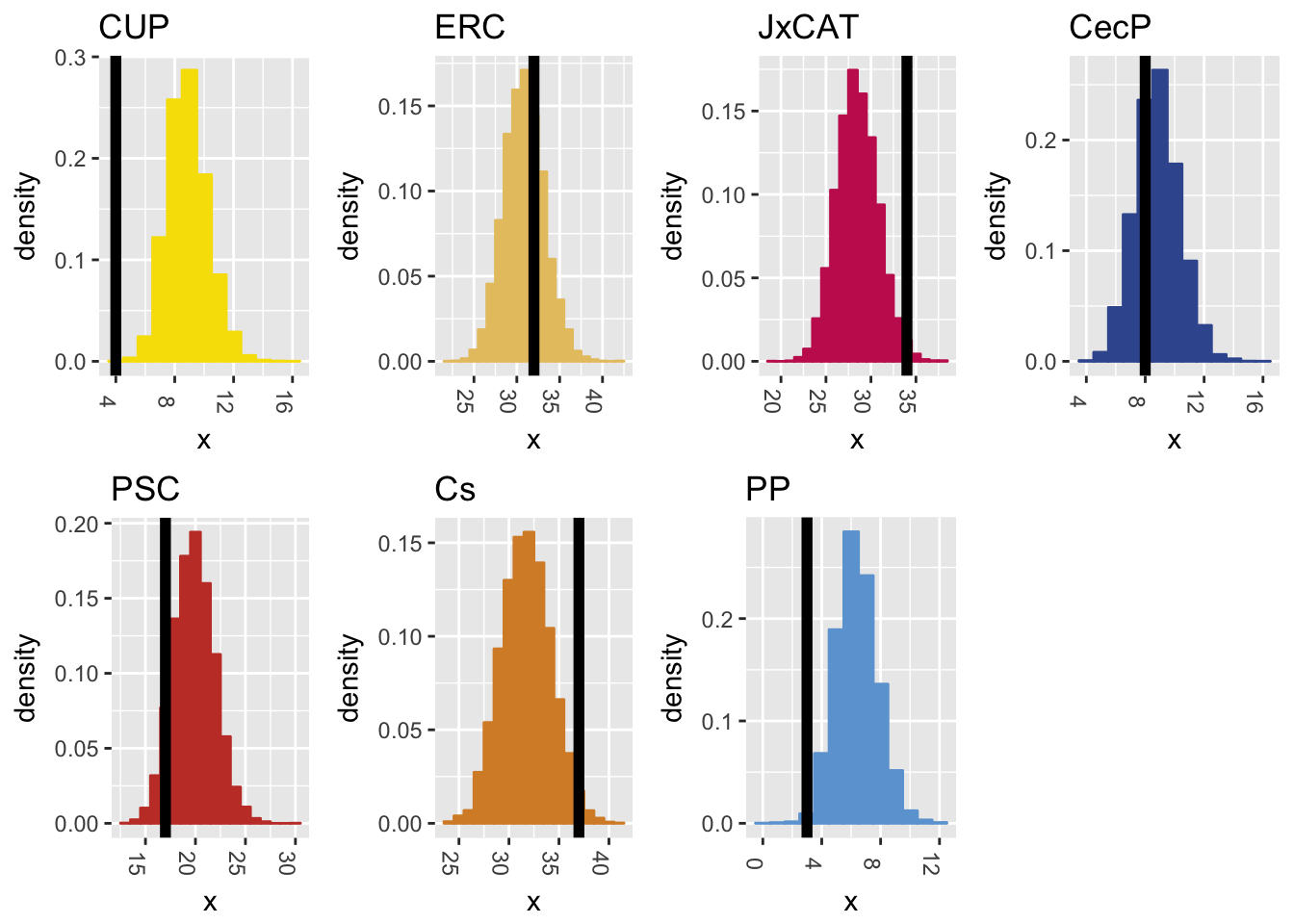
I’d say the coverage is good for most parties. Polls did not show the loss of voters for CUP and Partido Popular (PP).
Another nice thing of being Bayesian (and using MCMC) is that other probabilities could be computed. For example, the next plot shows the posterior distribution of the number of seats allocated to pro-independence parties so that the probability of them having a majority can be computed (59.86%):

As I promised to have a shot for each seat allocated correctly, I’ve got some work left to do until the end of the Christmas break… Merry Christmas and Happy New Year!!!